An insight to Decision Trees

Introduction

Decision trees are supervised learning models utilized for regression and classification. It uses a single tree that can be visualized so we can see the root, sub-roots, leaves, and the way the Tree has decided to predict/classify its final output gives decision trees high interpretability.

Types of Decision Trees

There are two varieties of Decision Trees based on the dependent variable:

1. Decision Tree Classifier: Here, the dependent feature is categorical, for instance, Diabetic and Non-Diabetic Patient, Fraudulent and non-fraudulent transactions.
2. Decision Tree Regressor: Here, the dependent feature is continuous like the income of a person, the percentage of effectiveness of a medicine.

Decision Tree for Regression

Decision trees where continuous values (typically real numbers) can be taken by the target variable are called regression trees. Via a process known as binary recursive partitioning, a regression tree is created, which is an iterative process that divides the data into partitions or divisions and then divides each section into smaller groups as each branch is moved by the system.

Suppose you have to predict the percentage of vitamin supplement effectiveness for a person based on the dosage, but the data when visualized shows that low dosages are not that significant, moderate are compelling up to 70%, somewhat higher are up to 50%, but very high dosages are not effective at all. We can’t fit a straight line in this case.

So one approach can be to fit a decision tree to this data, in this case, a regression-based tree.

Building Regression Tree

To select the root of the Tree, we try different threshold values based on the average of the data points(e.g., Dosage<14, Dosage<30, and so on.). We select the threshold, which gives the minimum sum of squared Residual difference (sum of the square of the difference between actual and predicted values) SSR as we can use the residuals to quantify the quality of the predictions.

In this way, we split the data in a way that reduces variance as we want homogeneous points in one leaf. We calculate the sum of squared residuals to decide the sub-roots similarly. It stops splitting when it has no more scope to reduce variance, but in real-world problems, we set the parameters and control the max_depth, min_samples_split, min_samples_leaf, etc. to make it robust as it needs to generalize better to be able to predict new data points.

Prune Regression Trees

To reduce overfitting, we use pruning.

• Cost-complexity Pruning: If we only use SSR to select the best Tree, the Tree will end up overfitting, so one way is to calculate the tree score, which takes no. of leaves into consideration while selecting the Tree.
• Weakest Link Pruning: Tree Score = SSR + alpha*(Terminal nodes) The tree complexity parameter(alpha) compensates for the difference in the no. of leaves, which is a more robust way to evaluate the score. Alpha is a tuning parameter which we can find cross-validation.

Decision Trees for Classification

Decision trees where the target variable is categorical are called classification trees. Suppose we want to classify if the person has diabetes or not. We have multiple features like Glucose, Blocked Arteries, Insulin, Skin Thickness, BMI, Age, etc. So want to use a decision tree for classification, how does it work? The Tree has three node types:

1. Root node: There are no incoming edges and zero outgoing edges or more.
2. Internal nodes: They have precisely one inbound edge and two outbound edges or more.
3. Leaf or terminal nodes: Precisely one incoming edge and no outgoing edges are possible.

First, it decides the primary root node. How? It starts by looking at how well feature 1 (Glucose) alone predicts! It will look at how well glucose separated patients with and without diabetes. It will do this process for all the features. And every Tree will have leaves which will have some no. of diabetic and some no. of non-diabetic people, for, e.g., if Age>50 has x no. of people diabetic people there might be y no. of people who do not have diabetes.

When none of the leaves is 100%, Yes or No, they are all considered impure. To determine which separation is best, we need a way to calculate the impurity index to measure and compare impurity.

Calculating Impurity

There are many ways to calculate impurity

• $$Entropy = \sum p_{j}log _{2} p _{j}$$
• $$Gini Index = 1 - \sum p _{j}2$$
• $$Classification Error = 1 - max(p _{j})$$

For the above example, let us choose the Gini Index to calculate impurity. For a leaf, the Gini Impurity =

1 - (probability of diabetic person)² - (probability of non diabetic person)²

Gini Impurity for Glucose as root node= Weighted average of Gini Impurities of the leaf nodes.

It calculates Gini impurity for every feature (where it as root), and then the feature with the lowest Gini impurity will be used as the root of the Tree. There will be further partitioning as the nodes are not 100% pure. So for finding sub-roots, it will again follow the same process.

Further, if the node itself seems to have the lowest score, then also partitioning is futile, and it becomes a leaf node. But if the segregation of the data results in the Gini score change, then the separation with the least level is picked.

• When the features are numeric like BMI:
  • Step 1: Sort the patients in ascending order.
  • Step 2: Calculate the average BMI for all adjacent patients.
  • Step 3: Calculate the impurity values for each average BMI. It will select the BMI value when the lowest impurity occurs.
• When a feature is of ranked data form: It is similar to numeric data but here impurity score is calculated for every rank.

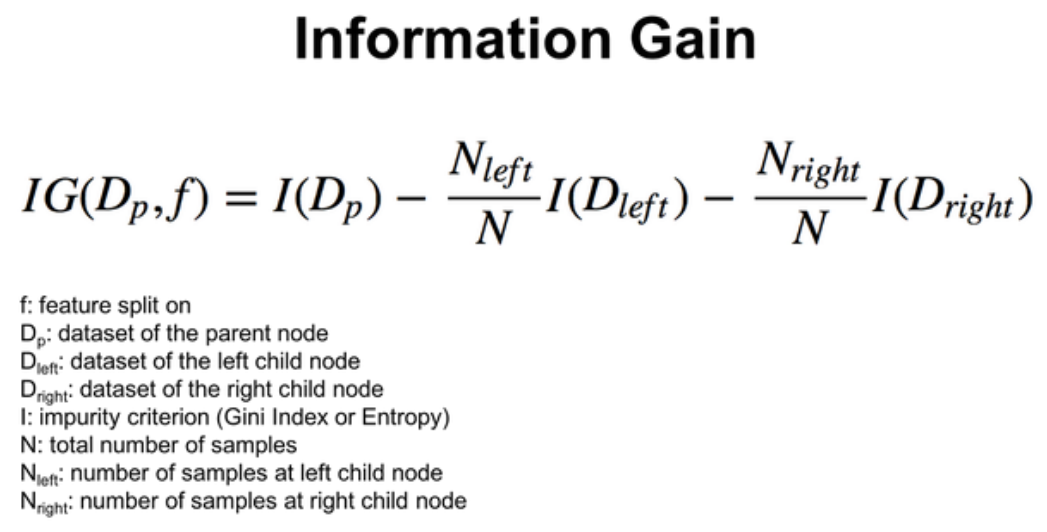
Information Gain should be highest when splitting the data.

Disadvantages/Limitations of Decision Trees

1. Locally greedy, tree splitting: The Tree looks for a binary division at each step so that the impurity of the Tree is reduced by the maximum number. It’s a greedy algorithm that hits the local optimum. For example, it may be likely to benefit less than the maximum decrease in impurity at the current level to achieve the lowest possible impurity of the final Tree, but the algorithm for tree splitting can not consider any more than the current level. This implies that the formulated Decision Tree is usually optimal locally and not optimal globally.
2. An optimal decision tree seems to be an NP-complete problem: The total number of trees from the same input dataset is exceedingly high because of the number of feature variables, the inherent abundance of split points, and the high depth of the Tree. Thus, not only is tree division, not global, but it is also virtually impossible to compute the ideal Tree globally.
3. Overfitting: Decision trees tend to overfit, which makes them less robust as they are sensitive and prone to sampling errors. It can be reduced by hyperparameter tuning like by setting the max-depth, min samples split, min samples leaf, max-leaf nodes, min impurity split. We can tune it using GridSearchCV and cross-validation and by evaluating different classification metrics to make it robust.