Tree Data Structure

Data structures are different ways in which we can store or organise data. They can be classified into broadly two types.

1. Linear Data Structures

Data structures in which data is stored in the sequential arrangement are called linear data structures. For example arrays, linked lists, queues etc. Please note that this does not imply storing data in consecutive locations. Data can be stored anywhere in the memory, though the linked list is a linear data structure, it does not store data in contiguous memory locations. By linear data structures, we mean that when we traverse the data structure then we will always get the values in a sequence.

2. Non-linear Data Structures

Non-linear data structure does not follow any sequence for storing data. Here data is stored hierarchically in multiple levels. Here computer memory is used more efficiently than linear data structures. E.g. trees, graphs

Trees

Tree is a hierarchical data structure. In tree data structure, data is stored in the form of nodes. Each node can be connected to zero or multiple nodes through edges. In this data structure, the arrangement of data resembles an inverted tree. It consists of one root node, branches and leaves. The root node is the node in the topmost layer while leaves are the nodes in the bottommost layer. Parent nodes are connected to their children through edges. Any node of a tree can have zero children or multiple children. E.g. in a binary tree any node can have minimum zero and at most two children. A N-ary tree can have minimum zero and at most n children.

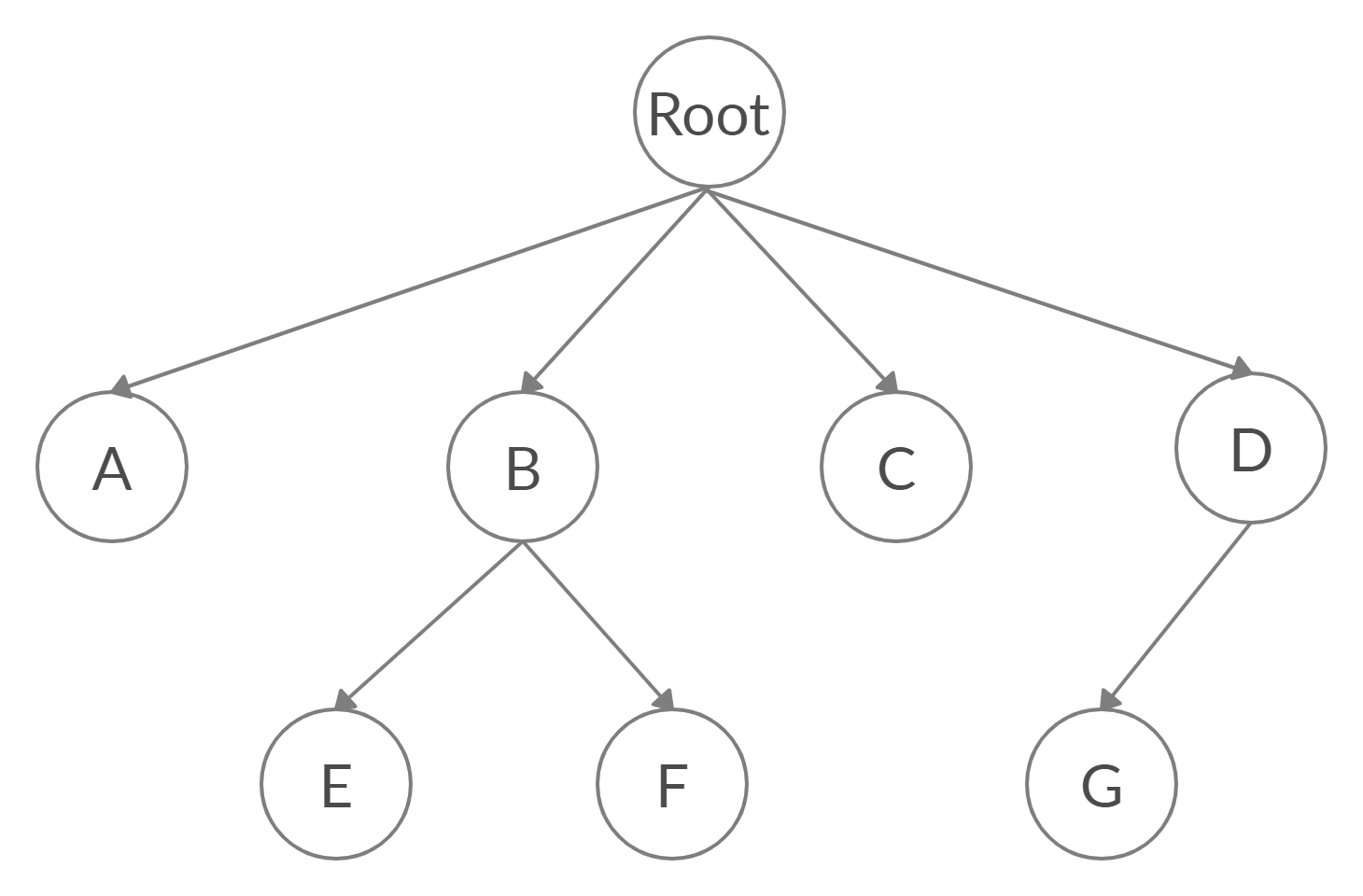
Binary Tree

Any node of a binary tree can have 0, 1 or at most 2 children. Every node in a binary tree has a parent node except the root node. Every node can have 0, 1 or 2 children except the leaf nodes which will have 0 children. In a binary tree, every node contains data and pointers to the left and right child nodes respectively.

Basic terminologies

• Root: node at the topmost level of the tree
• Leaf node: node at the bottommost level of the tree
• Edge: a line connecting parent node to the child node
• Parent node: node connected to the given node in the level above
• Child node: node connected to the given node in the level below
• Grandparent: parent of the parent node is called a grandparent
• Siblings: nodes having the same parent node
• Height: total no. of levels between the root node and the leaf in the bottommost level
• Depth: length of the path from the root to a particular node
• Subtree: any node and all its descendants form a subtree of the given tree

Structure of a binary tree node

struct tree {
  int data;
  struct tree *left;
  struct tree *right;
}

Basic Tree Functions

• Insert: insert a new node
• Search: search a node with the given key
• Delete: delete a node
• Preorder traversing: Access the root, then traverse the left subtree and later traverse the right subtree
• Inorder traversing: Traverse left subtree then access root and later traverse right subtree
• Postorder traversing: Traverse left subtree, then traverse right subtree and visit the root in the end

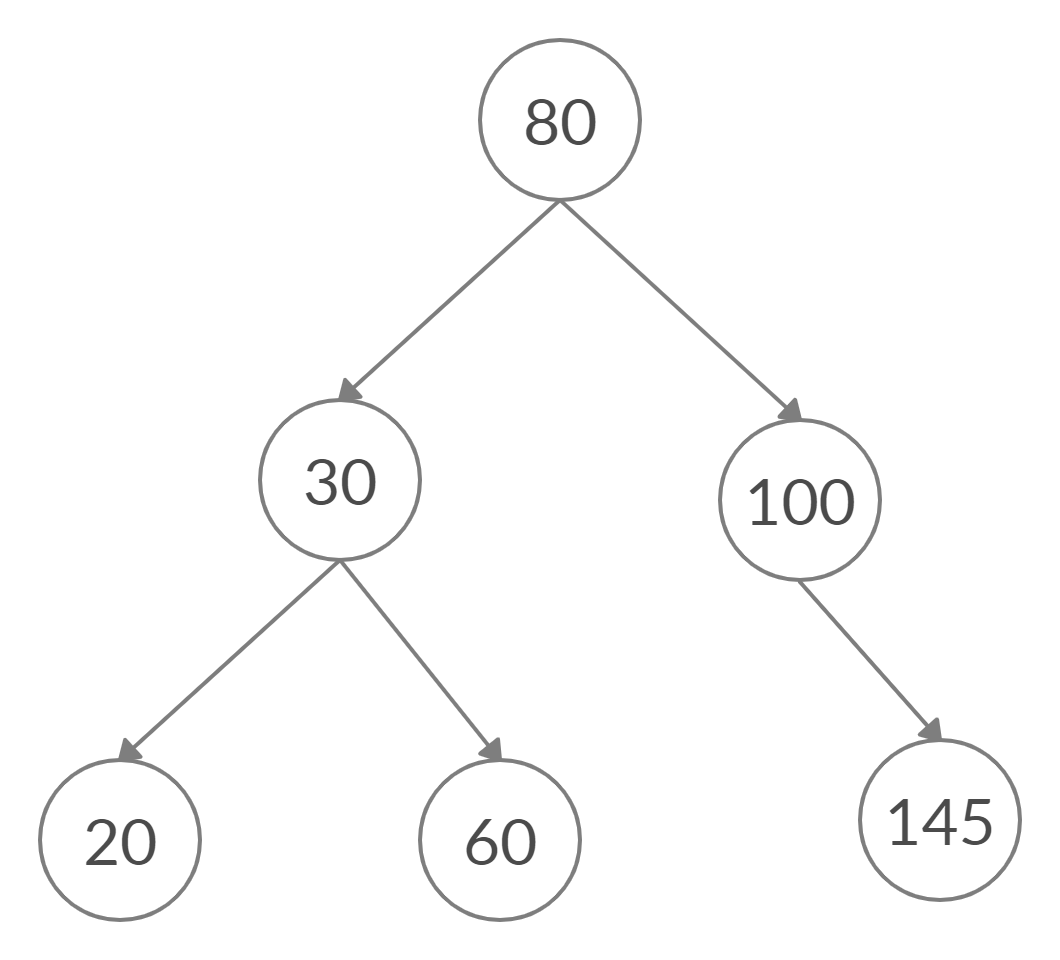
Binary Search Tree (BST)

These are special types of binary trees where the value of every node in the left subtree is less than the value of the root node as well as the value of every node in the right subtree is greater than the value of the root node. Binary search trees are very efficient for performing search operations. Operations like search, insertion and deletion can be done in trees in O(h) time where h is the height of the tree. AVL tree is a special type of binary search tree which maintains the height of a tree equal to log(n). Hence search complexity in case of AVL tree is always log(n).

The below image shows an example of a BST.