Radix Sort
Radix Sort is another sorting technique from the family of Linear Sorting Algorithms.
It sorts elements using their place values from the LSB (Least Significant Bit) to MSB (Most Significant Bit), we use Counting sort as a sub-routine to sort elements according to place values. We can also use any other sorting algorithms, but since Counting sort provides linear time complexity in this case, we prefer the same.
Understanding Radix Sort Algorithm
We already know how counting sort sorts elements by counting occurrences of respective elements, we use the same concept here but we don’t directly apply counting sort on elements, rather we apply it digit by digit, that is, first we apply on ones place, then on tens place, then hundreds and so on.
This gives us the sorted array in the end, and also we don’t have to create the count array of huge size, which was one of the main drawbacks of counting sort.
Radix Sort Algorithm
- Find the maximum element from the array
- Initialize exponent as 1
- Perform the below steps until (maximum element / exponent) > 0
- Call counting sort method with two parameters: Array and Exponent
- Multiply the value of exponent by 10 (This gives us place values as 1, 10, 100, and so on)
There will be a slight modification in the counting sort algorithm as now we to apply it digit by digit.
Counting Sort Algorithm
- Create Result Array and Count Array of the same size as of Array
- Iterate through each element of the given array, and for each occurrence of an element increment
count[(element / exponent) % 10]. - After the count of each elements’ digit is stored, cumulate the count array values, that is, find the cumulative frequency. This gives us the correct position of the respective digits.
Count[i]=Count[i]+Count[i-1] - Iterate
ifrom(lengthOfArray-1)to 0, and performResultArray[ Count[ (Array[i]/exponent) % 10 ] -1 ]=Array[i], after this decrement the count of element in count array.Count[ (Array[i] / exponent) % 10 ]-- - Copy values from Result Array to Array for the next iteration
Radix Sort Example
Consider an Array: 38, 21, 106, 56, 754, 2, 79, 74, 55, 6

Maximum Element = 754
Since the maximum element has three digits, therefore the counting sort method will be called thrice.
First Iteration
Exponent = 1
During the first method call, the values on which counting sort will be applied will be:
(Array Values / Exponent ) % 10
8, 1, 6, 6, 4, 2, 9, 4, 5, 6
After sorting these will look like:
1, 2, 4, 4, 5, 6, 6, 6, 8, 9
But remember these are not the actual values but only a single digit of those numbers.
So this is how the actual Array values will look:
21, 2, 754, 74, 55, 106, 56, 6, 38, 79
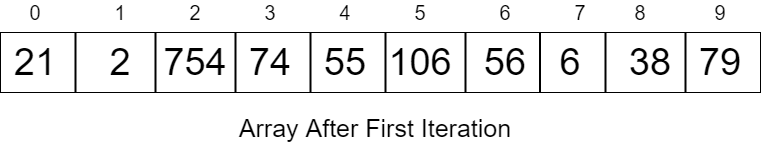
Second Iteration
Exponent = 10
Values for counting sort will be:
2, 0, 5, 7, 5, 0, 5, 0, 3, 7
After sorting the actual array values will look as:
2, 106, 6, 21, 38, 754, 55, 56, 74, 79
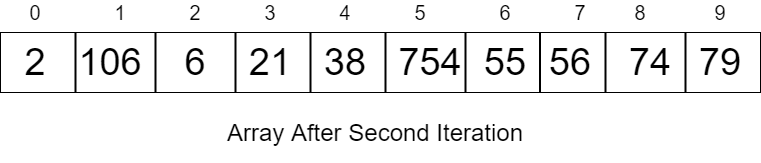
Third Iteration
Exponent = 100
Values for counting sort will be:
0, 1, 0, 0, 0, 7, 0, 0, 0, 0
Now we will get the final sorted array which will look like:
2, 6, 21, 38, 55, 56, 74, 79, 106, 754
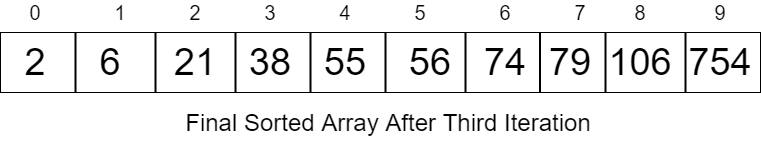
Code for Radix Sort
import java.util.Arrays;
class Sorting {
void radixSort(int arr[]) {
int max = arr[0];
int lengthOfArray = arr.length;
// Finding max element from the array
for (int i = 1; i < lengthOfArray; i++) {
if (max < arr[i]) {
max = arr[i];
}
}
int exp = 1;
// Calling countingSort method from the Least Significant Bit towards Most Significant Bit
while (max / exp > 0) {
countingSort(arr, exp);
exp = exp * 10;
}
}
void countingSort(int arr[], int exp) {
int lengthOfArray = arr.length;
int count[] = new int[lengthOfArray];
int resultArray[] = new int[lengthOfArray]; // array to store elements in sorted order
// storing count of respective elements
for (int i = 0; i < lengthOfArray; i++) {
count[(arr[i] / exp) % 10]++;
}
// calculating cumulative frequency
for (int i = 1; i < lengthOfArray; i++) {
count[i] = count[i] + count[i - 1];
}
// placing elements in their correct position
for (int i = lengthOfArray - 1; i >= 0; i--) {
resultArray[count[(arr[i] / exp) % 10] - 1] = arr[i];
count[(arr[i] / exp) % 10]--;
}
// since the countingSort method will be called again we need to assign sorted
// values in this pass in the Array back
for (int i = 0; i < lengthOfArray; i++) {
arr[i] = resultArray[i];
}
}
public static void main(String[] args) {
Sorting sort = new Sorting(); // creating object of class Sorting
int arr[] = { 38, 21, 106, 56, 754, 2, 79, 74, 55, 6, 14 };
sort.radixSort(arr); // method call
System.out.println("Array after applying Radix sort: " + Arrays.toString(arr));
}
}Performance
| Case | Runtime |
|---|---|
| Best | O(n) |
| Average | O(dn) |
| Worst | O(dn) |
| Auxiliary Space | O(n) |
Here d is the number of digits in the maximum element.
Help us improve this content by editing this page on GitHub