Merge Sort

Merge sort is a popular sorting algorithm which uses divide and conquer algorithm. Consider an array A to be sorted. We divide the array A into two parts and sort them individually. The heart of the Merge Sort is a procedure called Merge. Let’s see the Merge procedure first and then we will use Merge as a subroutine to implement Merge Sort algorithm.

Merge Procedure

Here sub-array_1 A[p,q] and sub-array-2 A[q+1,r] are sorted individually and we want to sort them as a whole.

• Len1 = q-p+1 and Len2 = r-q
• Create two separate lists of sizes of Len1+1 and Len2+1
• Copy the two sorted part of the arrays into the lists
• Add infinity to the end of both lists (the maximum number the data structure can support)
• Take 3 pointers i, j, k where i & j point to first elements of both the lists and k points to the first element of the original array A

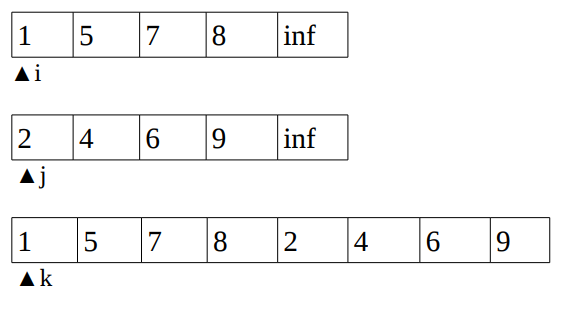
• Now we will fill the array A(basically overwrite) in a sorted manner.
• Compare the elements at i and j. Whichever is smaller (say i), copy its value to kth index in array A and then increment pointers k and i (we considered ele(i) <ele(j)).
• We repeat the above process till k does not reach the end of the array A.
• Compare (1,2) and then increment i and k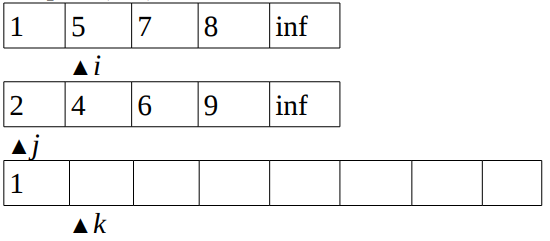
• Compare (5,2) and then increment j and k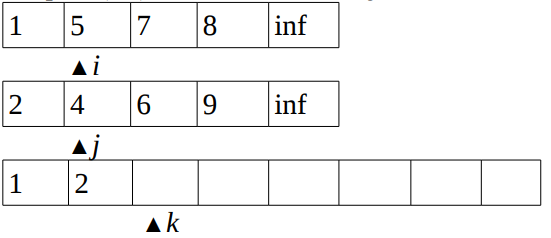
• Compare (5,4) and then increment j and k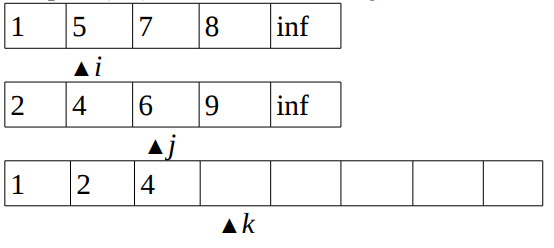
• Compare (5,6) and then increment i and k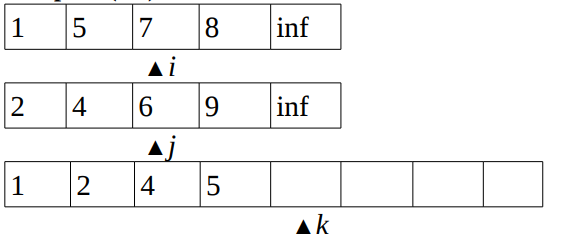
• Compare (7,6) and then increment j and k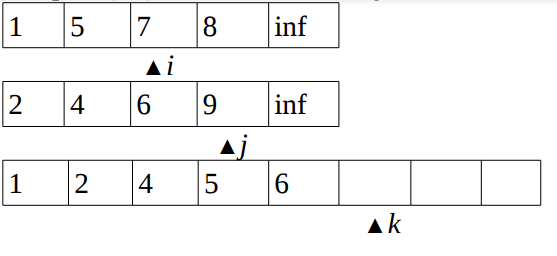
• Compare (7,9) and then increment i and k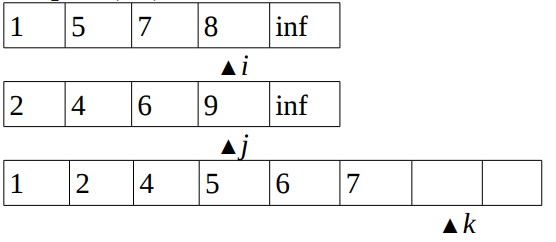
• Compare (8,9) and then increment i and k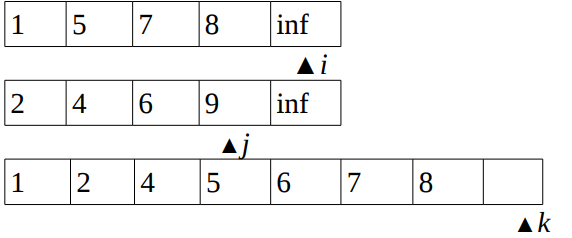
• Compare (inf,9) and then increment j and k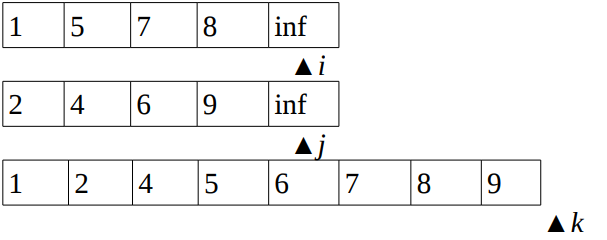
• Thus by the end of the Merge procedure the two individually sorted sub_array gets sorted as a whole in the original array A

Psuedo code for Merge Sort procedure

Merge(A, p, q, r) {
    // Consider all arrays as 1-indexed arrays
    n1 = q - p + 1
    n2 = r - p
    let Left[1.......n1 + 1] and Right[1.........n2 + 1] be two new arrays
    for (i = 1 to n1) // to copy the first sorted list into array Left "O(N / 2)"
    {
        Left[i] = A[p + i - 1]                          
    }
    for (j = 1 to n2) // to copy the second sorted list into array Right "O(N / 2)"
    {
        Right[i] = A[q + j]                             
    }
    Left[n1 + 1] = inf
    Right[n2 + 1] = inf
    i = 1, j = 1
    for (k = p to r) { // "O(N / 2)"
        if (Left[i] <= Right[j]) {
            A[k] = Left[j]
            i++
        }
        else {
            A[k] = Right[j]
            j++
        }
        k++
    }
}

Time complexity of merge procedure

time taken = O(n/2 + n/2 + n) = O(n)

Space complexity of merge procedure:

extra space = O(n/2 + n/2) // for two extra arrays Left and Right = O(n)
Now, we have an array A consisting on n elements. Let T(n) be the time required to sort the array.

Psuedo code for Merge sort

Merge_sort(A, p, r) {
    if (p < r) {
        q = floor((p + r) / 2)  // find the mid point
        Merge_sort(A, p, q)     // T(n / 2)
        Merge_sort(A, q + 1, r) // T(n / 2)
        Merge(A, p, q, r)       // T(n)
    }
}

Time complexity of merge sort

T(n) = time taken to sort n sized array
We divided the array into two n/2 sized array and sorted them individually.
So, time taken to sort those two sub arrays = T(n/2) + T(n/2) = 2T(n/2)
Merging the two arrays of size n/2 into an array of size n requires calling of the merge procedure which requires a time of O(n)
So, we come to the following recursive equation: T(n) = 2*T(n/2) + O(n)
Using Master’s theorem, we get T(n) = O(n.logn)

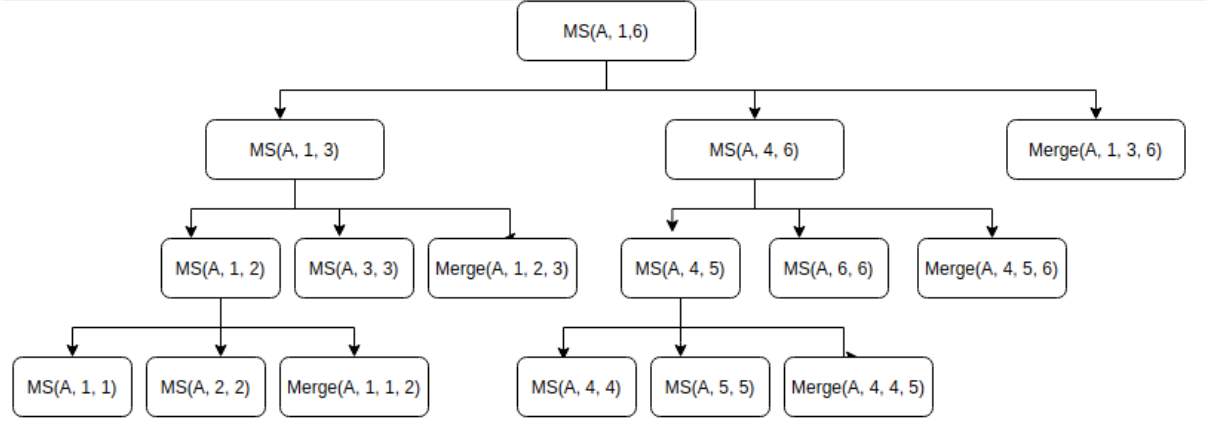
Recursive tree

• Consider an array with 6 elements. The array is 1-indexed, thus p=1 and r=6. Let MS represent the Merge_sort function and Merge as usual represents our Merge function.
• We see that the total number of function call here is 16.
• The height of the tree is floor(log2n) + 1. Substitute n = 6, we get four levels as shown

Space complexity of merge sort

• We don’t consider the space required for variables p, q, r, i, j as they require constant space. The input array is already given. Thus, it is not considered in the extra space required category.
• The procedure Merge requires two new lists of size n/2 every time it is called on an array of size n. Instead of creating two list space every time, we can use as a global array of O(n) space for copying of elements. It can be used by every call to procedure Merge one by one.
  (1) Thus space required for Merge is O(n)
• The other extra space used during merge sort is the stack space for recursive function calls. Now in our example, for n=6, the number of function calls was 16
• But, do we really need a stack with 16 activation records entries? Turns out, we don’t really need a stack of height 16.

• All the function calls in the same level in the recursion tree ocuupy the same cell of the stack. Thus we have a stack of height equal to the height of the tree.
  Height of stack = Height of the recursive tree

  • For n sized array
  • Number of levels = floor(log2n) + 1
  • Assume each cell of stack( Activation record) is ok size k.
    
  • (2) Stack Size = (floor(log2n) + 1)*k = O(k*log2n) = O(log2n)
  • From (1) and (2)
  • Space Complexity = n + log2n = O(n)

Note

• Merge sort falls under the category of out-of-place sorting algorithm since we need extra space for sorting (extra space is needed in the merge procedure, thus it is not in-place)
• Merge sort is a stable sorting algorithm as the algorithm used in our pseudo code doesn’t change the relative position of same valued elements