Interpolation Search
No doubt Binary Search is one the best searching algorithms providing average runtime of O(log n), but still there are cases where more efficient searching could be performed.
Let’s discuss one such scenario.
Consider two arrays:
Array 1: 1 3 8 9 12 14 27 29 34 37
Array 2: 10 20 30 40 50 60 70 80 90 100 110 120
Both of the above arrays are sorted in ascending order, but if you observe closely Array 1 is not uniformly distributed, but Array 2 is uniformly distributed, that is, the elements in Array 2 are placed in regular intervals of equal size, in our case 10.
Now if we want to search element 110 in Array 2, and we go by the normal binary search it will first select the middle element and then reach 110 dividing array into half each time.
But we know the array is uniformly distributed, therefore it will be beneficial if we initiate search towards the right side. This is what the Interpolation Search does, it does not always select the middle element but rather selects the element based on the data being searched.
What is Interpolation?
Interpolation is a mathematical term, which is basically a process of estimating an intermediate value given some set of discrete values.
Understanding Interpolation Search
Interpolation search is an optimized version of vanilla Binary Search, which is best suited for uniformly distributed values.
Almost the whole algorithm is similar to that of binary search, except selecting the pivot point or probe which is selected based on the value being searched.

Interpolation Search Algorithm
- Find the probe using the formula
- Compare it with the data
- If the value is matched, return success
- If the value is smaller, select the left sub-array and repeat steps from starting
- If the value is greater, select the right sub-array and repeat steps from starting
- Repeat the above steps, if the element is found return success otherwise return failure
The above algorithm works for elements sorted in ascending order, for descending order if the value is greater select the left sub-array and vice versa.
Example
Consider the Array: 7 10 13 17 20 23 26 29 32
Element to search: 29

Now we will find the probe using the formula.
Initially
low=0, high=8
mid = 0 + (((8-0)/(32-7))*(29-7))
mid = 6In this case, we can see that the probe is right-biased as the required value is on the right side of the array, similarly, if the value would have been on the left side of the array, the probe value would have been left-biased.
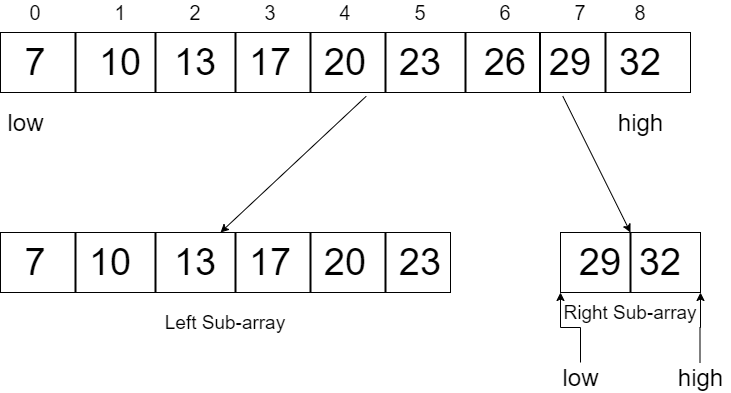
low=7, high=8
mid = 7 + (((8-7)/(32-29))*(29-29))
mid = 7Here arr[mid] = 29 which is the required element, hence we converge to the result in just two passes.
Now let’s have a look at the Java code for Interpolation Search.
Code
public class Searching {
boolean interpolationSearch(int arr[], int n) {
int lengthOfArray = arr.length;
int mid; // to store middle element
int low = 0;
int high = lengthOfArray - 1;
while (low <= high) {
mid = low + (((high - low) / (arr[high] - arr[low])) * (n - arr[low])); // Formula for finding the pivot point or probe
if (arr[mid] == n) {
return true;
} else if (arr[mid] < n) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return false;
}
// Driver Code
public static void main(String args[]) {
Searching search = new Searching();
int arr[] = {
12,
16,
25,
37,
46,
55,
76,
86
};
if (search.interpolationSearch(arr, 76)) {
System.out.println("Element found !");
} else {
System.out.println("Element not found :( ");
}
}
}Performance
| Case | Runtime |
|---|---|
| Best | O(1) |
| Average | O(log(log n)) |
| Worst | O(n) |
| Auxiliary Space | O(1) |
Interpolation search works best when the values are uniformly distributed and can converge to the result in an average runtime of O(log (log n)).
Help us improve this content by editing this page on GitHub