Exponential Search
The term Exponential generally denotes rapid growth, and mathematically it means increasing in powers.
For example:
Exponential growth of 2: 2^0, 2^1, 2^2, 2^3, 2^4 and so on => (1, 2, 4, 8, 16,…..)
Exponential growth of 3: 3^0, 3^1, 3^2, 3^3, 3^4 and so on => (1, 3, 9, 27, 81,….)
We use the same generated numbers ( powers of 2 ) to jump indexes in array and get closer to the index of key.
In this algorithm, ultimately we rely on Binary Search for searching, but before that, we finalize a range in which the element we want to search might be present.
To finalize this range we follow a certain algorithm, let’s have a quick look at the overview of working of this algorithm with the help of an example.
Understanding Exponential Search
Consider a sorted Array: 7 12 34 57 65 74 81 88 89 93 100
Element to search: 93
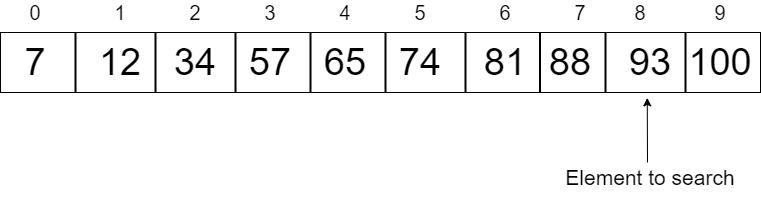
We will start by comparing the first element of the array with the key.
But Array[0]=7, which is not equal to 93.
Now we will take a variable whose value will increase exponentially, hence the name, exponential search.
int i= 1 ( because 2^0=1)
Now we will see if Array[i] is less than or equal to the key.
If it is, then we will keep on increasing the value exponentially.
i=i*2
This will generate values in powers of 2. ( 2, 4, 8, 16, 32...)
We will keep on increasing the value of i, until the condition Array[i]<=key is satisfied.
So in the above example, the value of i will reach 8 (in the actual code it will reach 16, then we will divide it by 2) and the sub-array after this index will be selected (including the index of i), and then the binary search will be applied to this range.
Exponential Search Algorithm
There are majorly two steps included in implementing exponential search:-
- Finding the range in which the key might lie
- Applying binary search in this range
Steps
- Start with value
i=1 - Check for condition
i < nandArray[i]<=key, wherenis the number of elements in the array and key is the element being searched - Increment value of i in powers of 2, that is,
i=i*2 - Keep on incrementing the value of
iuntil the condition is satisfied - Apply binary on the range
i/2till the end of Array -binarySearch(Array, i/2, min(i,n-1))
Example
Consider the array:- 1 3 5 7 9 11 13 15 17 19
Element to search: 19
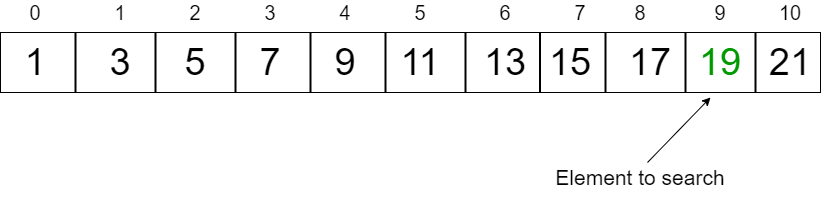
- We will start by comparing
Array[0]element to key, which in our case would return false. iwill be initialized to1
Now we will keep on incrementing the value of i until it is less than or equal to the key
After 1st pass i will be 2 - condition satisfied
After 2nd pass i will be 4 - condition satisfied
After 3rd pass i will be 8 - condition satisfied
After 4th pass i will be 16 - CONDITION FAILEDNote that the value of i is now 16, and the index 16 is out of range in this case, so to get the previous value of i we will divide it by 2, and call binary search using index of low as i/2.
Now we call the binary search method.
binarySearch(Array, i/2, min(i, n-1), key)

low = 8, high = 10
mid = (low + high)/2
= 18/2
= 9Array[9]=19, which is the required element.
Now let’s have a look at the Java code for the same.
Code
public class Searching {
boolean exponentialSearch(int arr[], int key) {
int lengthOfArray = arr.length;
if (arr[0] == key) { // Checking whether first element is the key
return true;
}
// Finding the range in which the element might be present
int i = 1;
while (i < lengthOfArray && arr[i] <= key) {
i = i * 2; // Exponentially increasing value of i.
}
return binarySearch(arr, i / 2, Math.min(i, lengthOfArray - 1), key); // calling binary search method on the sub-array
}
boolean binarySearch(int arr[], int low, int high, int key) {
int mid; // to store middle element
while (low <= high) {
mid = (low + high) / 2; // we can also do mid = low+(high-low)/2 to avoid overflow in some cases
if (arr[mid] == key) {
return true;
} else if (arr[mid] < key) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return false;
}
// Driver Code
public static void main(String args[]) {
Searching search = new Searching();
int arr[] = {
1,
3,
4,
6,
8,
13,
15,
24
};
if (search.exponentialSearch(arr, 15)) {
System.out.println("Element found !");
} else {
System.out.println("Element not found :( ");
}
}
}Performance
| Case | Runtime |
|---|---|
| Best | O(1) |
| Average | O(log i) |
| Worst | O(log i) |
| Auxiliary Space | O(1) |
Here i is the index of the key.
Exponential search is useful in cases where the arrays are unbounded or of infinite size and can converge to the solution much faster than binary search in these cases.
Help us improve this content by editing this page on GitHub