Counting Sort
Counting sort is one of the very few sorting algorithms that can sort elements in almost linear time.
It works by counting the frequency of elements, storing it in an auxiliary array, and finding an appropriate place for each element with the help of this count array.
Counting sort works best for small range values, but its linear time complexity doesn’t guarantee that it will work faster than other sorting algorithms in all cases, as the length of count array is equal to the max element of the array, which can turn out to be very large at times.
Understanding Counting Sort Algorithm
The basic idea of working of this algorithm is counting how many elements are smaller than a particular element, with the help of this we can directly place the element in its correct position without any comparisons.
For example, if we know that ‘4’ elements are less than ‘13’ in a certain array, then the correct place for 13 will be 5th ( index 4 ).
Counting Sort Algorithm
- Consider an array of size ‘n’, having elements in range (0-k)
- Create an integer array of size ‘k’ and initialize its all elements to 0 ( We will call this array count)
- Iterate through each element of the given array, and for each occurrence of an element increment count[element]. For example, if the element is 3 then we will increment count[3],
- After the count of each element is stored, cumulate the count array values, that is, find the cumulative frequency. This gives us the correct position of elements. Count[i]=Count[i]+Count[i-1]
- Iterate i from (lengthOfArray-1) to 0, and perform ResultArray[ Count[ Array[i] ] -1 ]=Array[i], after this decrement the count of element in count array. Count[ Array[i] ]–
Counting Sort Example
Consider an array: 7 4 3 4 6 7 2 5

Now we will create a count array of size 8 (since elements are in range 0-7), whose all elements will be initialzed to 0.
After counting each element the count array will look like:
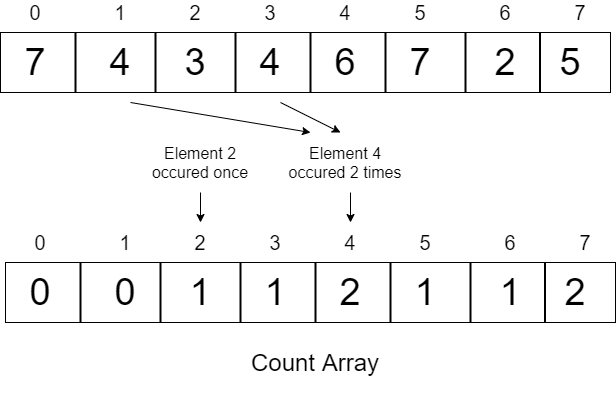
Now we will compute the cumulative count, that is, use the previous two values and add them to compute the current value.
The count array after computing all cumulative value will look as follows:
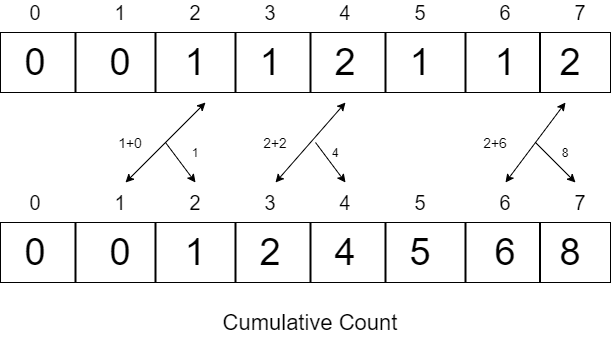
After having cumulative count we can compute the correct position of respective elements as follows:-
i= (lengthOfArray-1 to 0)
i= 7 to 0
i=7
resultArray [count [Array[i]] - 1] = Array[i]
resultArray[ count [Array[7]]-1] = Array[7]
resultArray[ count[5]-1] = 5
resultArray[4]= 5
count[5]--
count[5]=4
i=6
resultArray [count [Array[i]] - 1] = Array[i]
resultArray[ count [Array[6]]-1] = Array[6]
resultArray[ count[2]-1] = 2
resultArray[0]= 2
count[2]--
count[2]=0
i=5
resultArray [count [Array[i]] - 1] = Array[i]
resultArray[ count [Array[5]]-1] = Array[5]
resultArray[ count[7]-1] = 7
resultArray[7]= 7
count[7]--
count[7]=7
i=4
resultArray [count [Array[i]] - 1] = Array[i]
resultArray[ count [Array[4]]-1] = Array[4]
resultArray[ count[6]-1] = 6
resultArray[5]= 6
count[6]--
count[6]=5
i=3
resultArray [count [Array[i]] - 1] = Array[i]
resultArray[ count [Array[3]]-1] = Array[3]
resultArray[ count[4]-1] = 4
resultArray[3]= 4
count[4]--
count[4]=3
i=2
resultArray [count [Array[i]] - 1] = Array[i]
resultArray[ count [Array[2]]-1] = Array[2]
resultArray[ count[3]-1] = 3
resultArray[1]= 3
count[3]--
count[3]=1
i=1
resultArray [count [Array[i]] - 1] = Array[i]
resultArray[ count [Array[1]]-1] = Array[1]
resultArray[ count[4]-1] = 4
resultArray[2]= 4
count[4]--
count[4]=2
i=0
resultArray [count [Array[i]] - 1] = Array[i]
resultArray[ count [Array[0]]-1] = Array[0]
resultArray[ count[7]-1] = 7
resultArray[6]= 7
count[7]--
count[7]=5Now the result array will be the required sorted array, which will look as follows:
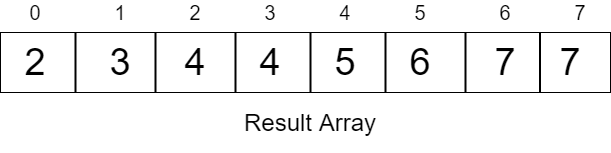
Now that we know how Counting Sort works, let’s look at the code for the same.
Code for Counting Sort
public class Sorting {
int[] countingSort(int arr[], int k) {
int lengthOfArray = arr.length;
int count[] = new int[k + 1];
int resultArray[] = new int[lengthOfArray]; // array to store elements in sorted order
// storing count of respective elements
for (int i = 0; i < lengthOfArray; i++) {
count[arr[i]]++;
}
// calculating cumulative frequency
for (int i = 1; i <= k; i++) {
count[i] = count[i] + count[i - 1];
}
// placing elements in their correct position
for (int i = lengthOfArray - 1; i >= 0; i--) {
resultArray[count[arr[i]] - 1] = arr[i];
count[arr[i]]--;
}
return resultArray;
}
public static void main(String[] args) {
Sorting sort = new Sorting(); // creating object of class Sorting
int[] arr = { 7, 4, 3, 4, 6, 7, 2, 5 };
arr = sort.countingSort(arr, 7); // method call
System.out.println("Array after applying Counting sort : " + Arrays.toString(arr));
}
}Performance
| Case | Runtime |
|---|---|
| Best | O(n) |
| Average | O(n+k) |
| Worst | O(n+k) |
| Auxiliary Space | O(n+k) |
Here k is the upper limit of the range of elements.
The main advantage of counting sort is its linear time complexity which works very well for small range elements.
But consider a case where there might be values in thousands. In this case, we will have to create a count array of thousands of size, and also perform thousands of operations, which will make complexity worse than most of the sorting algorithms.
Hence it is advisable to go with counting sort only if the number of elements is small and range of elements is less.
Help us improve this content by editing this page on GitHub