Binary Search

Generally if we are asked to perform searching, what we do is take every element one by one and compare with the input value. This in computing terms is called Linear Search.

But do we really need to compare to every element in, specially in cases where number of elements are huge?

Let’s take an example of dictionary. Now we know that a dictionary contains thousands of words, and if we are required to search a particular word, we don’t go scanning every word in dictionary, but follow a planned approach and get towards the required word.

But one thing to note here is that, words in dictionary are organized in alphabetical order, therefore it becomes easy to search a particular word.

Today we will discuss one such searching technique called Binary Search, it is generally used if the elements provided are pre-sorted either in ascending or descending order.

Understanding the Algorithm

What we basically do in this searching technique is select a middle element from the array and divide the array in two parts. Left side contains elements which are smaller than the middle element (in case of ascending) and right side contains elements greater than middle element.

If the element to search is smaller than middle element, then we discard the right side and vice versa. And if the middle element is the element that we are finding, then we stop our searching.

This process of partitioning the array into two parts and comparing the middle element is continued until we find our element.

Let’s have a deeper look at the algorithm:

1. Find middle element in the array.
2. Compare it with the given value.
3. If it matches, return success
4. If the given element is smaller, select the left sub-array and perform the steps from 1.
5. If the given element is greater, select the right sub-array and perform the steps from 1.
6. Repeat the steps until the element is found or only one element is left in the sub-array.

Please note that the above algorithm is applicable for elements stored in ascending order, in case of descending order, if element is smaller than middle element then right sub-array will be selected and vice versa.

Example

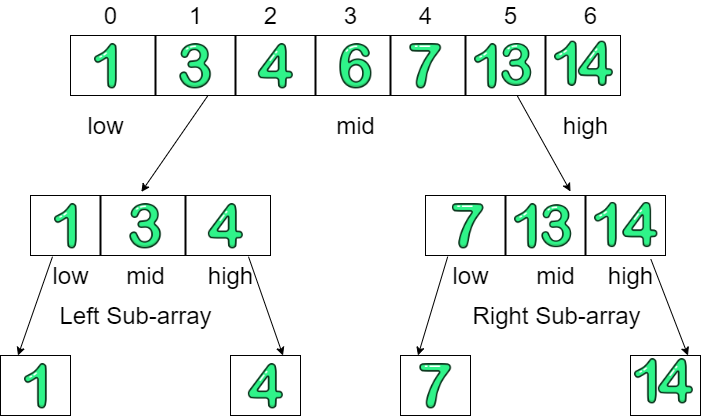
Consider the array: 1 3 4 6 7 13 14 Element to search: 13

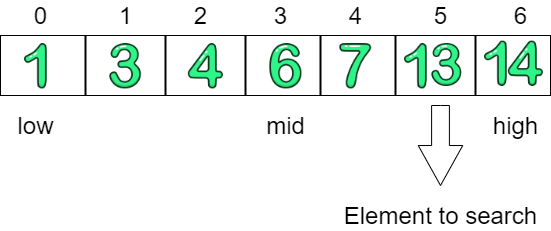
First we find the middle element from the array, and we get 6.

Now, 13 is greater than 6, therefore we will select the right sub-array, i.e, 7 13 14

Again we perform the search operation on this sub-array, and this time we get 13 as middle element, which is the desired element in our case.

So, we saw it only took 2 passes to find the element which would have otherwise taken 6 passes in case of linear search.

Code

public class Searching {

    boolean binarySearch(int arr[], int n) {
        int lengthOfArray = arr.length;
        int mid; // to store middle element
        int low = 0;
        int high = lengthOfArray - 1;
        while (low <= high) {
            mid = (low + high) / 2; // we can also do mid = low+(high-low)/2 to avoid overflow in some cases
            if (arr[mid] == n) {
                return true;
            } else if (arr[mid] < n) {
                low = mid + 1;
            } else {
                high = mid - 1;
            }
        }
        return false;
    }

    // Driver Code
    public static void main(String args[]) {
        Searching search = new Searching();
        int arr[] = {
            1,
            3,
            4,
            6,
            8,
            13,
            15,
            24
        };
        if (search.binarySearch(arr, 45)) {
            System.out.println("Element found !");
        } else {
            System.out.println("Element not found :( ");
        }

    }
}

The above code was iterative, now let’s have a look at recursive code for the same.

Recursive code for Binary Search

public class Searching {

    boolean binarySearch(int arr[], int low, int high, int n) {

        int mid = (low + high) / 2;

        if (low > high) {
            return false; // base condition
        }

        if (arr[mid] == n) {
            return true;
        } else if (arr[mid] < n) {
            return binarySearch(arr, mid + 1, high, n); // recursive call to right sub-array
        } else {
            return binarySearch(arr, low, mid - 1, n); // recursive call to left sub-array
        }

    }

    // Driver Code
    public static void main(String args[]) {

        Searching search = new Searching();

        int arr[] = {
            1,
            3,
            4,
            6,
            8,
            13,
            15,
            24
        };

        int lengthOfArray = arr.length;

        if (search.binarySearch(arr, 0, lengthOfArray - 1, 125)) {
            System.out.println("Element found !");
        } else {
            System.out.println("Element not found :( ");
        }

    }
}

Performance

• Worst Case Time Complexity: O(log n)
• Average Case Time Complexity: O(log n)
• Best Case Time Complexity: O(1)
• Space Complexity: O(1)

Important points to note

• Binary search can only be applied to sorted elements.
• If the elements are unsorted, we need to sort them first to apply binary search.
• Binary search is a type of divide and conquer algorithm.
• Binary search is better for large amounts of data.
• There might be cases where linear search would perform better than binary search.