Binary Search Tree

Previous article gave the Introduction to Trees and BST. This article will explain some important operations on BST.

Binary Search Trees are special types of binary trees where the value of every node in the left subtree is less than the value of the root node as well as the value of every node in the right subtree is greater than the value of the root node.

Structure

Structure of a BST node is like following:

struct BST {
    int data;
    struct BST *left;
    struct BST *right;
};

Some important BST Functions:

1. Creating new node

struct BST* createNode(int value)
{
    struct BST* newNode = (struct BST*)malloc(sizeof(struct BST));
    newNode->data = value;
    newNode->left = NULL;
    newNode->right = NULL;
    return newNode;
}

2. Inserting a new node in the BST

struct BST* insert(BST* root,int value)
{
    if(root==NULL)
    return createNode(value);
 
    if(value<root->data)
    root->left = insert(root->left,value);
    else
    root->right = insert(root->right,value);
 
    return root;
}

3. Inorder Traversal

void inOrder(struct BST* root)
{
    if(root!=NULL)
    {
        inOrder(root->left);
        cout<<root->data<<" ";
        inOrder(root->right);
    }
}

4. Preorder Traversal

void preOrder(struct BST* root)
{
    if(root!=NULL)
    {
        cout<<root->data<<" ";
        preOrder(root->left);
        preOrder(root->right);
    }
}

5. Postorder Traversal

void postOrder(struct BST* root)
{
    if(root!=NULL)
    {
        postOrder(root->left);
        postOrder(root->right);
        cout<<root->data<<" ";
    }
}

6. Finding the minimum node

According to the property of the BST, the value of every node in the left subtree of the current node should be less than the value of the current node. Hence, this property is used while finding the minimum node in a BST. We reach to the leftmost node in the BST which has the minimum possible value in the BST.

struct BST* findMinNode(struct BST* root)
{
    struct BST* temp = root;
    while(temp->left!=NULL && temp)
    temp = temp->left;
    return temp;
}

7. Deleting a node

For deleting a node, first of all, we need to reach that node. The function does this by recursively calling itself within the function. When we are reached to that particular node to be deleted there are 3 possible cases:

  1. The node is a leaf node
  2. The node has a single child
  3. The node has 2 children

After deleting a node we must replace it by its inorder successor or inorder predecessor to maintain the property of BST.
So if the node belongs to the first 2 cases then we return a pointer to the right subtree or left subtree whichever is available and free that node. Both the left and right subtree pointers are anyways going to be NULL in case of leaf nodes. Hence they will also get deleted.
If the node belongs to the third case then we replace its value with the value of the inorder successor. We use findMinNode function which returns the inorder successor. Then we replace the value of the node with the value of inorder successor and delete the inorder successor.

struct BST* deleteNode(struct BST* root, int value)
{
    if(root == NULL)
    return root;
 
    if(value<root->data)
    root->left = deleteNode(root->left,value);
    else if(value>root->data)
    root->right = deleteNode(root->right,value);
    else
    {
        if(root->left==NULL)
        {
            struct BST *temp = root->right;
            free(root);
            return temp;
        }
        else if(root->right==NULL)
        {
            struct BST *temp = root->left;
            free(root);
            return temp;
        }
 
        struct BST *temp = findMinNode(root->right);
        root->data = temp->data;
        root->right = deleteNode(root->right,temp->data);
    }
    return root;
}

Driver program to test the above functions:

int main()
{
    struct BST *root = NULL;
    root = insert(root,50);
    root = insert(root,100);
    root = insert(root,30);
    root = insert(root,70);
    root = insert(root,40);
    root = insert(root,60);
    root = insert(root,20);
 
    cout<<"Inorder traversal of initial BST"<<endl;
    inOrder(root);
 
    root = deleteNode(root,40);
    cout<<"\nAfter deleting node with value 40"<<endl;
    inOrder(root);
 
    root = deleteNode(root,60);
    cout<<"\nAfter deleting node with value 60"<<endl;
    inOrder(root);
    return 0;
}

Output:

Inorder traversal of initial BST
20 30 40 45 50 70 100 120
After deleting node with value 40
20 30 45 50 70 100 120
After deleting node with value 100
20 30 45 50 70 120

Illustration

  • Initial BST "diagram of initial BST"
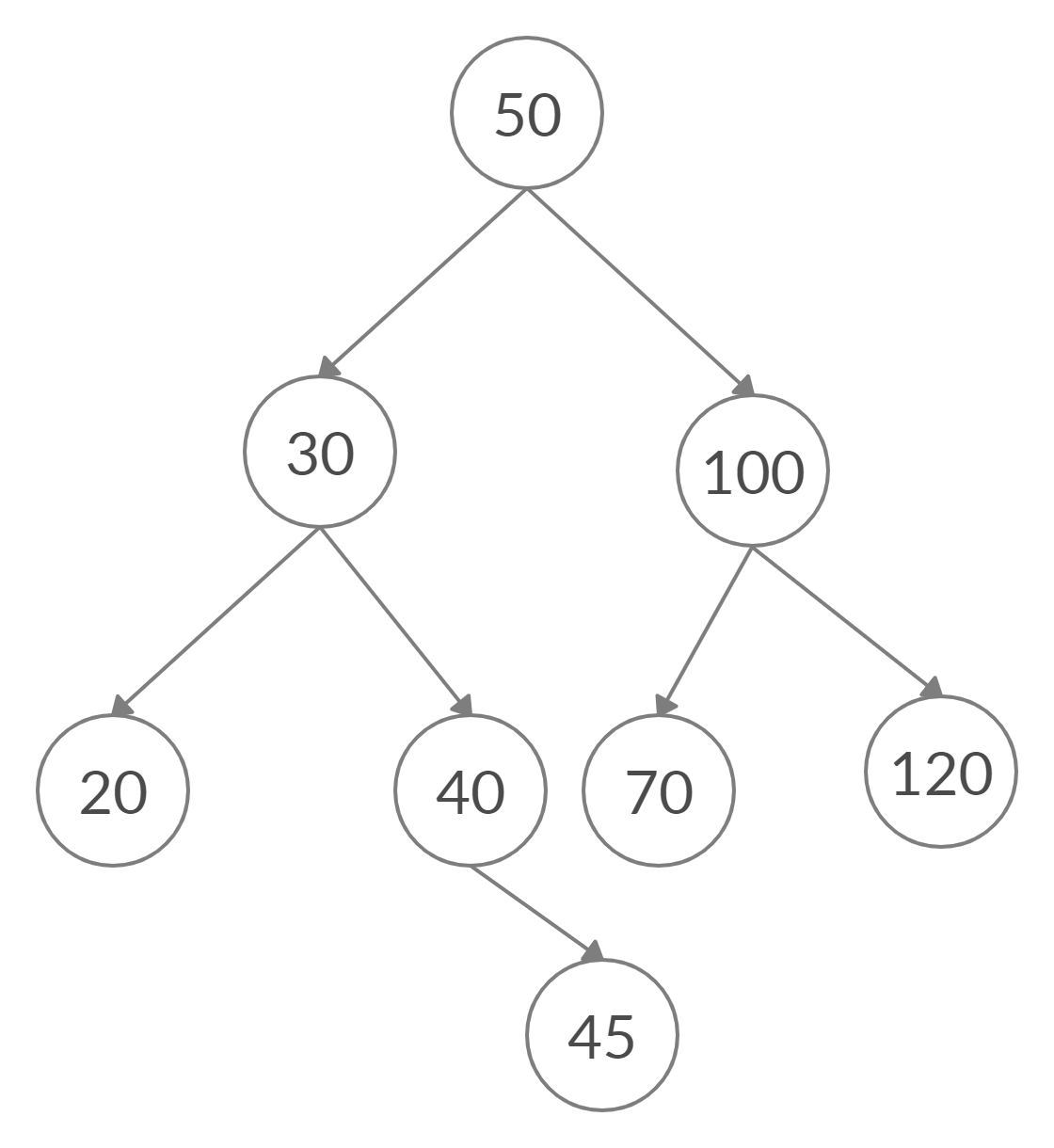
  • After deleting node with value 40 "diagram after deleting 40"
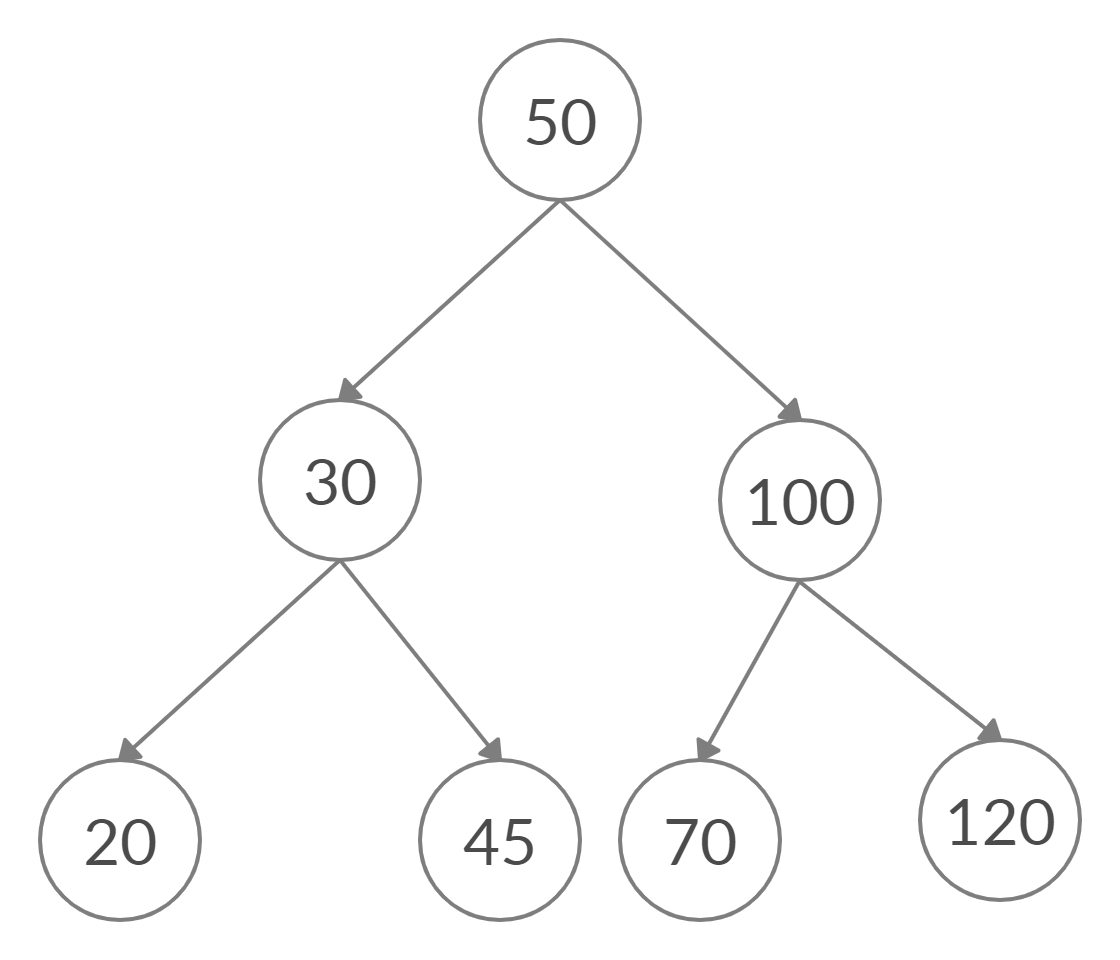
  • After deleting node with value 100 "diagram after deleting 100"

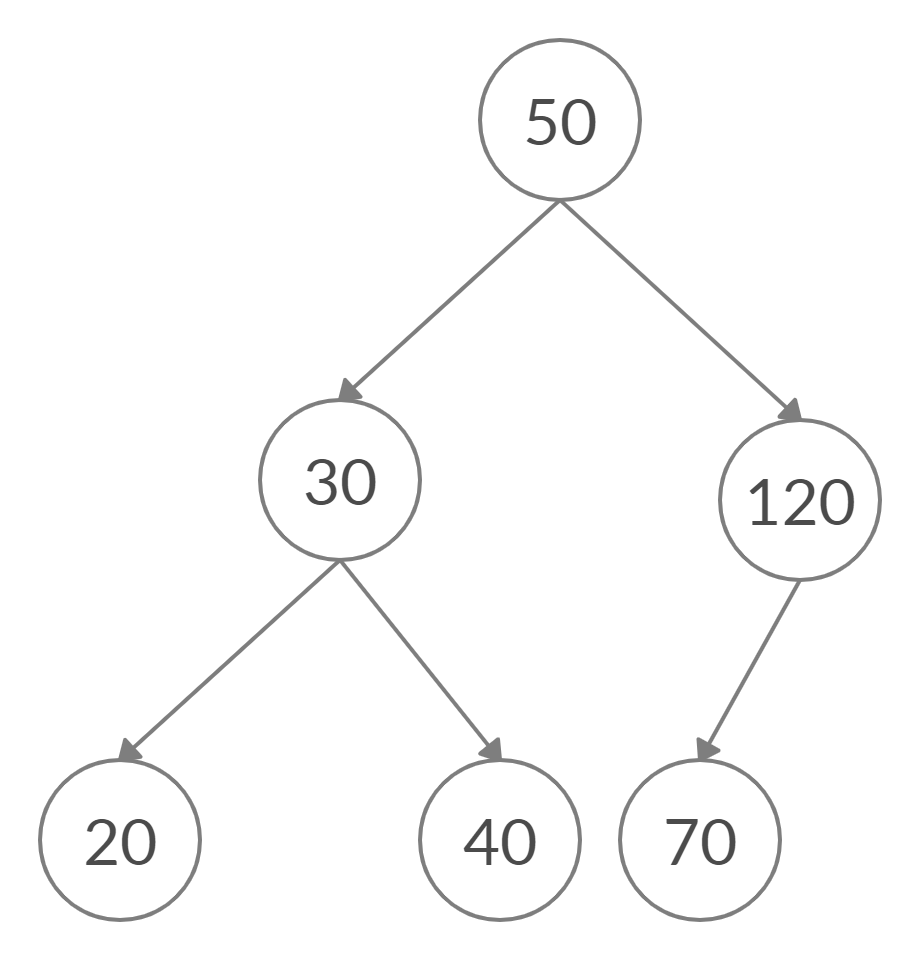
Help us improve this content by editing this page on GitHub